Projekt von: Anne Elenz, Sven Harder, Christina
Hochreiter, Katja Stark
1. Einleitung
1.1. Was ist eine
Spirale?
1.2. Woher kennen wir Spiralen, wo treten
diese in der Natur, in der
Technik, im Alltag und in der Kunst auf?
1.2.1. Spiralen in der Natur
1.2.2. Spiralen in
der Technik
1.2.3. Spiralen im Alltag
1.2.4. Spiralen in der Kunst
1.3. Historisches
zu Spiralen
1.3.1. Die Archimedische Spirale
1.3.2. Die Logarithmische Spirale
1.3.3. Sonstige Spiralen
2. Die Archimedische Spirale
2.1.
Einführung und Definition
2.2. Formel und
Eigenschaften
2.3. Flächenberechnung
2.4. Anwendungsbeispiele
3. Die Logarithmische Spirale
3.1. Einleitung
3.2. Konstruktion der logarithmischen Spirale
3.3. Weitere Eigenschaften der logarithmischen Spirale
4. Überblick über Spiraltypen
4.1.
Hyperbolische Spirale
4.2. Fermatsche Spirale
4.3. Krummstab (bzw. Lituus)
4.4.
Weitere Arten von Spiralen
4.4.1. Galileische
Spirale
4.4.2. Spirale dritten Grades in r
4.4.3. Spirale dritten Grades in j
5. Didaktischer Aspekt
5.1. Thema
Spirale im Schulunterricht
5.2. Verschiedene Ansätze
zur Einführung in die Spiralentheorie
5.2.1. Spiralen
zeichnen mit dem Zirkel (Archimedische Spirale)
5.2.2.
Praktisches Beispiel anhand dem Modell "Raupe auf der
Uhr" (Archimedische Spirale)
6. Konstruktion eines "Spiralen – Zeichen – Gerätes"
7. Aufgaben
8. Anlage
9. Literaturverzeichnis
1. Einleitung
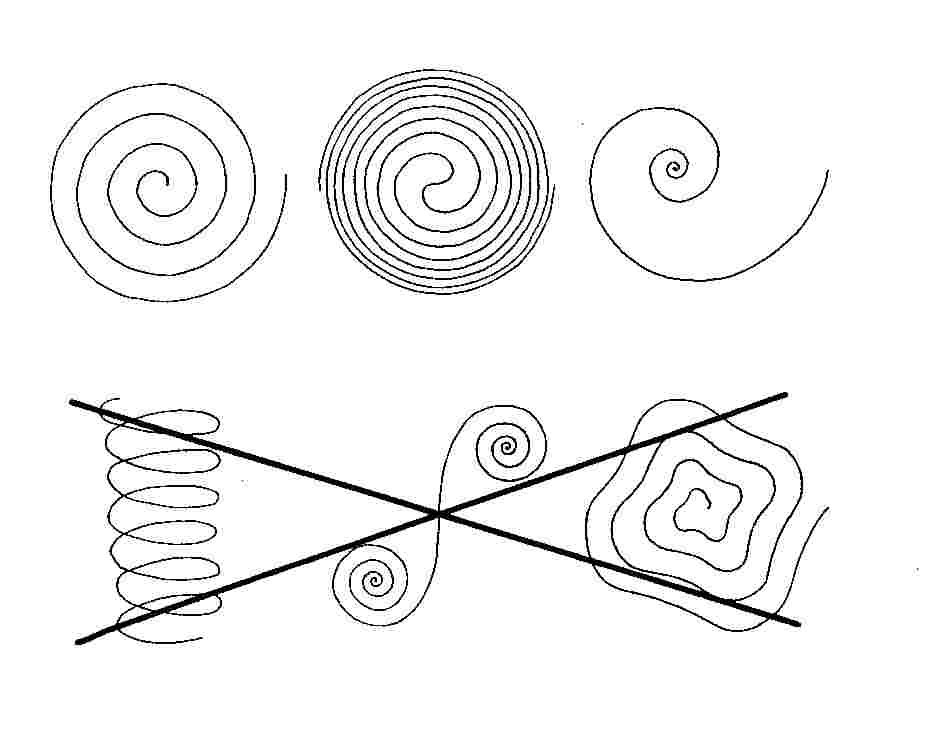
1.1. Was ist eine Spirale?
Warum sind die drei Abbildungen oben Spiralen und die drei unten nicht?
Es gibt verschiedene Definitionen, je nachdem, ob man den ganzen Definitionsbereich wählt oder nicht. Im Folgenden werden zwei aufgelistet:
Def.: Unter einer Spirale versteht man eine Kurve, zu der es
eine Polardarstellung r = f (j )
gibt mit einer
stetigen und streng monotonen Funktion f.
Def.: Eine Spirale ist eine ebene Kurve, die aus unendlich
vielen Windungen um einen festen
Punkt besteht und aus höchsten zwei Ästen
zusammengesetzt ist, bei denen der Abstand
vom Mittelpunkt streng monoton
vom Drehwinkel abhängt.
Aus den beiden Definitionen lässt sich erkennen, dass der Begriff von den alltäglichen Vorstellungen abweicht. Im Alltag denkt man – wenn man Spirale hört - an Schrauben, Federn, Wendeltreppen, .... In den obigen Definitionen ist aber von ebenen Figuren die Rede.
Es werden Euch die archimedische Spirale, die logarithmischeSpirale, die hyperbolische Spirale, die Fermatsche Spirale, der Krummstab, die Galileische Spirale und die Spiralen höheren Grades vorgestellt.
Um Spiralen mathematisch zu beschreiben ist es sinnvoll die Darstellung in Polarkoordinaten zu verwenden.
1.2. Woher kennen wir Spiralen, wo treten diese in der Natur, in der
Technik, im Alltag und in der Kunst auf?
3) Elefanten können z.B. ihren Rüssel in eine spiralige Form winden, um etwas
zu greifen
und Schlangen winden sich oft spiralförmig um etwas für ihren
Temperaturhaushalt zu tun.
4) Auch als Bewegungsbahnen gibt es Spiralen in der Tierwelt, z.B. Spinnen
bauen so ihr
Nest.
5) Fast jeder Mensch hat einen oder mehrere Haarwirbel. Dies sind auch
Spiralphänomene.
Dies ist aber noch nicht alles beim Menschen. Die
Nabelschnur eines Neugeborenen ist oft
spiralig gewunden, die Schnecke im
Innenohr ist spiralförmig oder sogar im Fingerabdruck
sieht man Spiralen.
6) Auch im Wasser oder in der Luft treten spiralförmige Bewegungen auf, z.B.
beim Wasser-
strudel oder beim Ablaufstrudel in der Badewanne. Auch im
Wetterbericht im Fernsehen,
erkennt man bei der Luftströmung um ein
Tiefdruckgebiet spiralförmige Bewegungen.
1.2.1. Spiralen in der Natur
In der Natur treten Spiralen in dreierlei Variationen auf. Einmal als feste
Form, einmal als momentane Position und einmal als Bewegungsbahn.
1.2.2. Spiralen in der Technik
In der Technik tritt öfter die Schraubenlinie auf, aber es gibt auch Spiralen. Z.B. bei aufgewickelten Tauen, bei Papierrollen, bei Drahtgeflechten, Pumpen und Turbinen sind meistens spiralförmig, ...
Auch hier gibt es spiralförmige Bewegungsbahnen, z.B. müssen Weltraumraketen
auf Spira-len zur Erde zurückkehren, da sie sonst verglühen würden.
1.2.3. Spiralen im Alltag
Hier kann man z.B. an folgende Sachen denken:
1. Topfuntersetzer
2. Kuchenrost
3. Kassetten
4. Brotkörbchen
5. Verband
6. Schallplatte
7. Geige, wo man am Geigenkopf die sogenannte Schnecke sehen kann
Wenn ein Kuchen mit Sahne verziert wird, wird auch oft mit einer Tortenspritze eine Spirale gespritzt.
Jeder kennt Autobahnabfahrten. Diese dürfen nicht zu stark um die Kurve gehen, da die Autos mit hoher Geschwindigkeit dort einfahren. Auch dort wird die geforderte Situation von einer Spirale erfüllt.
Ein weiteres Beispiel ist im Sport zu finden, und zwar beim Sprinten. Dort müssen die Startblöcke der Läufer, wenn sie in einem Stadion auf einer 400m Bahn laufen, auf einer hyperbolischen Spirale liegen, damit sie bis zur Zielgeraden die gleiche Entfernung zurückgelegt haben.
Auch in Comics wird das Symbol der Spirale benutzt und zwar als Symbol für Flüche.
Man könnte noch vieles aufzählen, aber das würde hier den Rahmen sprengen.
1.2.4. Spiralen in der Kunst
Besonders im antiken Griechenland lassen sich viele Spiralen in Kunst und
Architektur finden. Z.B. bei der ionischen Säule lassen sich die spiralförmigen
Köpfe erkennen. Es treten sowohl archimedische als auch logarithmische Spiralen
auf.
Bei Mosaiken kann man auch oft spiralförmige Figuren entdecken.
In der Malerei kann man folgende Künstler nennen, die immer wieder
spiralförmige Figuren bei ihren Arbeiten verwendet haben: Leonardo da Vinci
(1452 – 1519), Albrecht Dürer (1471 – 1528), Vincent van Gogh (1853 – 1890),
Paul Klee (1879 – 1940), ....
Faszinierend ist, dass es praktisch keinen Kulturkreis und keine Epoche gibt,
wo die Spirale in der Kunst nicht vorhanden ist. In vielen Kulturen hat das
Spiralsymbol tiefe religiöse oder mystische Bedeutung. Darauf sei hier nur
hingewiesen, aber aus zeitlichen Gründen nicht näher darauf eingegangen.
1.3. Historisches zu Spiralen
1.3.1. Die archimedische Spirale
Benannt ist sie nach Archimedes, der von 287 – 212 v. Chr, in Syrakus auf Sizilien gelebt hat und Hofmathematiker des Königs Hieron war. Archimedes war nicht nur Mathematiker, sondern auch Physiker und Techniker. Er hat zum Thema Spiralen sogar eine Abhandlung geschrieben, welche "Über Spiralen" hieß. Die archimedische Spirale ist nach der Quadratix des Hippias von Chios die zweitälteste bekannte kinematisch erzeugte Kurve.
600 Jahre später war es Pappos, der sich wieder mit der archimedischen Spirale befasst hat. Z.B. beweist er, dass sich die Fläche der Spirale zu der des Kreises genauso verhält wie das Volumen des Kegels zu dem des Zylinders.
Albrecht Dürer, der 1471 – 1528 lebte, beschäftigte sich mit Näherungskonstruktionen.
Als nächste beschäftigten sich Viète, der von 1540 – 1603 in Frankreich lebte und Jurist war und Souvey, der von 1577 – 1629 in der Schweiz und in Italien lebte sich mit Spiralen und zwar mit der Spirale als Quadratrix und Souvey fasste die Erkenntnisse antiker Mathematik zusammen.
Von Cavalieri stammt folgender berühmte Satz:
Liegen zwei Körper zwischen zueinander parallelen Ebenen E1 und E2 und werden sie von jeder zu E1 parallelen Ebene E‘ so geschnitten, dass gleich große Schnittflächen entstehen, so haben die Körper das gleiche Volumen.
Weiter Personen, die sich mit der archimedischen Spirale beschäftigt haben werden jetzt nur noch aufgezählt:
Pascal, Vincentius, Varignon, Torricelli, Fermat, Roberval, L’Hospital, Guldin, Barrow, Cotes, Angelis, Clairaut, ...
1.3.2. Die logarithmische Spirale
René Descartes, der von 1596 – 1650 lebte, gilt als Begründer der analytischen Geometrie. 1638 erläuterte er die logarithmische Spirale, die allerdings schon bei Albrecht Dürer (1471 – 1528) vorkommt. Auch Torricelli (1608 – 1647) kam mit Descartes zeitgleich auf diese Spirale. Ihr Name stammt von Varignon (1654 – 1722)
Weitere Personen, die sich mit der logarithmischen Spirale beschäftigt haben werden jetzt nur noch aufgezählt:
Jakob Bernoulli, Johann Bernoulli, Huygens, Newton, Leibniz, Collins, Barrow,
Euler, ...
Dazu folgende Zeitleiste:
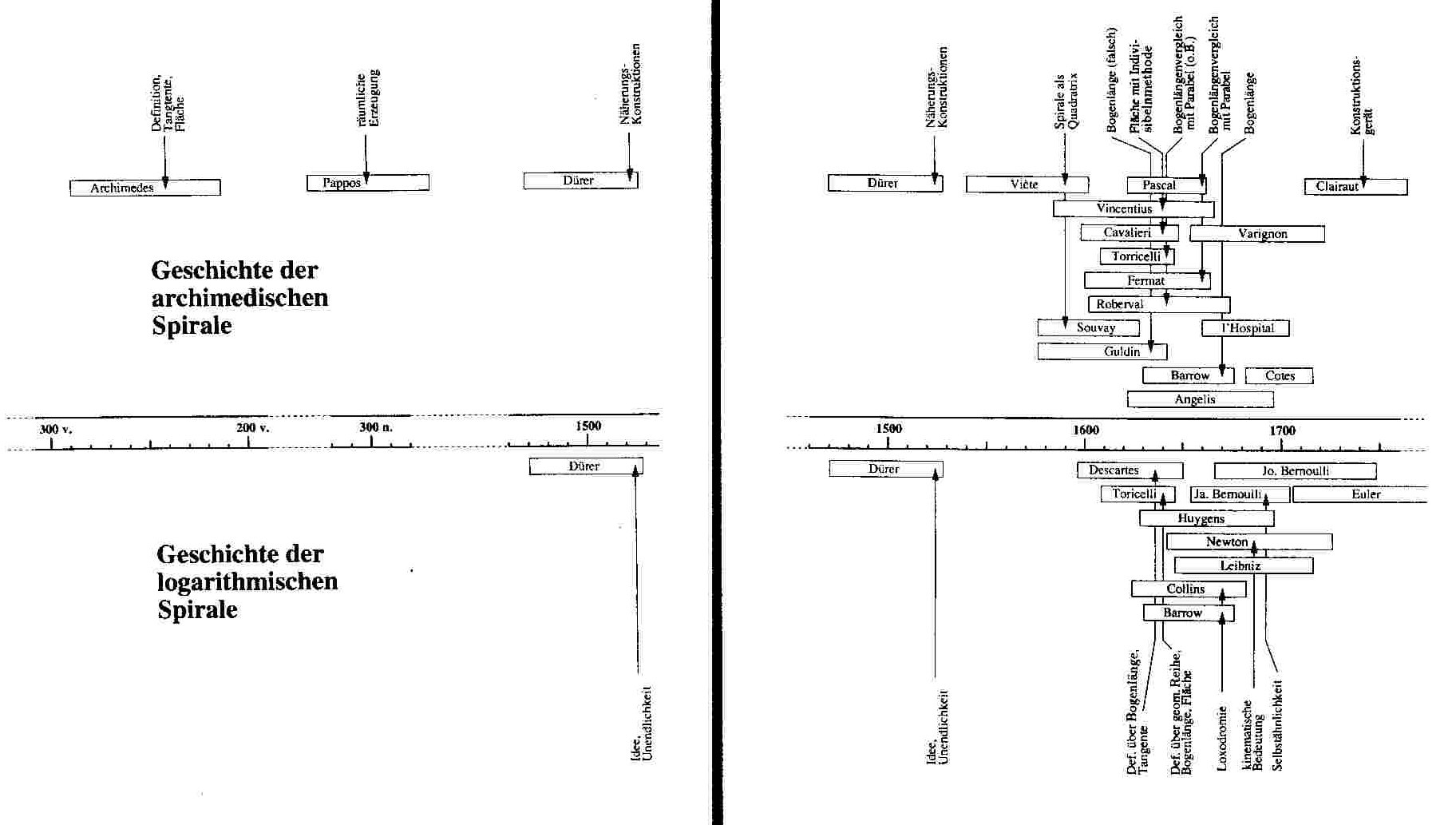
1.3.3. Sonstige Spiralen
Die Hyperbolische Spirale wurde zuerst von Varignon (1654 – 1722) und Johann Bernoulli (1667 – 1748) untersucht.
1636 wird die Fermatsche Spirale zum ersten Mal in einem Brief von Pierre de Fermat erwähnt.
Roger Cotes (1682 –1716) untersuchte als erster den Krummstab (oder Lituus).
2. Die Archimedische Spirale
2.1. Einführung und Definition
Archimedes schreibt in seiner Abhandlung "Über Spiralen":
"Wenn ein Halbstrahl sich innerhalb einer Ebene um seinen Endpunkt mit gleichförmiger Geschwindigkeit dreht, bis er wieder in seine Ausgangsstellung zurückkehrt, gleichzeitig aber sich ein Punkt auf diesem Halbstrahl mit gleichförmiger Geschwindigkeit vom Endpunkt des Halbstrahls aus bewegt, so wird der Punkt eine Spirale beschreiben."
Entstehung einer solchen Spirale
Um zu einer Definition für die Archimedische Spirale zu kommen, betrachtet
man zunächst das "Raupenmodell", das einen kinematischen Zugang liefert.
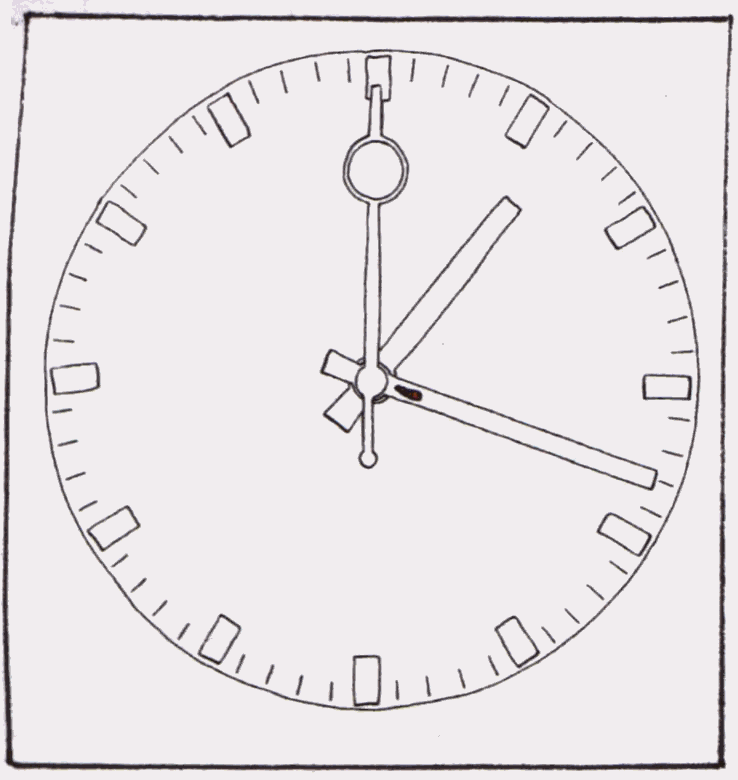
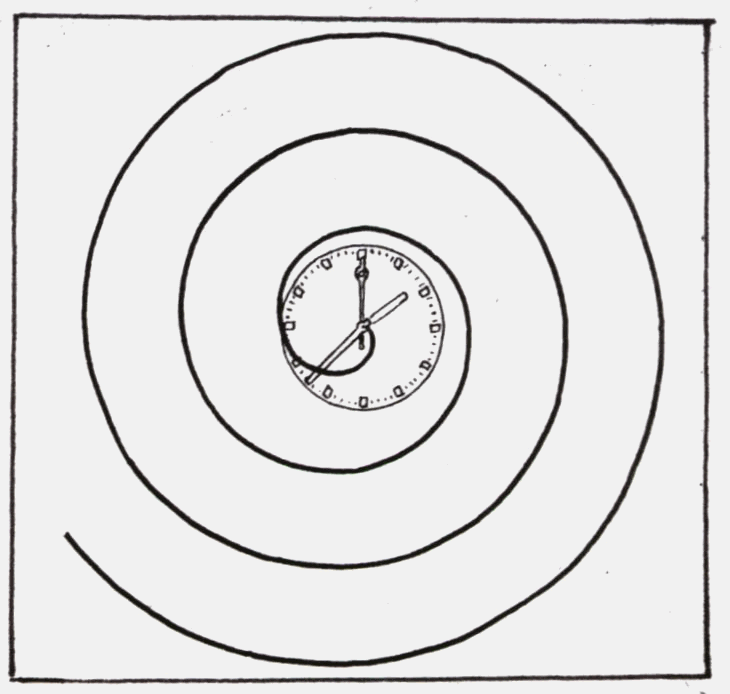
Abb.1 : Raupe auf der Uhr Abb.2 : Bahn der Raupe
Auf dem Minutenzeiger einer großen Uhr befindet sich eine Raupe. Der
Minutenzeiger bewege sich dabei mit konstanter Winkelgeschwindigkeit 
= 2
/60min, die Raupe krieche mit der
konstanten Geschwindigkeit v
=1cm/min auf dem Zeiger nach außen, wobei der Zeiger unendlich lang sei.
Die entstehende Bahn der Raupe stellt eine Überlagerung zweier stetiger
Bewegungen dar (Kreisbahn und Halbgerade). Diese Bahn ist eine Spirale mit
konstantem Windungsabstand, man nennt sie Archimedische Spirale.
Definition:
Eine Archimedische Spirale ist die Bahn eines Punktes, der sich auf einem mit
konstanter Winkelgeschwindigkeit w
¹ 0 rotierenden Halbstrahl mit
konstanter Geschwindigkeit v
¹ 0 vom Zentrum nach außen bewegt.
Nach der Quadratrix des Hippias von Chios(ca.460 v.Chr.) ist die Archimedische Spirale die zweitälteste bekannte kinematisch erzeugte Kurve, d.h. hier wirken sowohl zwei verschiedene Arten von Bewegung(linear und zirkular), als auch zwei verschiedene bewegte Elemente (Punkt und Gerade) zusammen.
2.2. Formeln und Eigenschaften
Die Gleichung der Archimedischen Spirale lässt sich leicht mit dem Raupenmodell herleiten: Man kann für jeden Zeitpunkt die Entfernung der Raupe vom Mittelpunkt direkt in Abhängigkeit vom Drehwinkel des Zeigers angeben und so den Zeitparameter t eliminieren.
Die Gleichung der Archimedischen Spirale in Polarkoordinaten lautet :
r = aj mit j
IR\IR
, aIR
wobei: a =
0:
Quotient der erzeugenden Geschwindigkeiten,
r
: der am Ende der
ersten Windung erreichte Radius
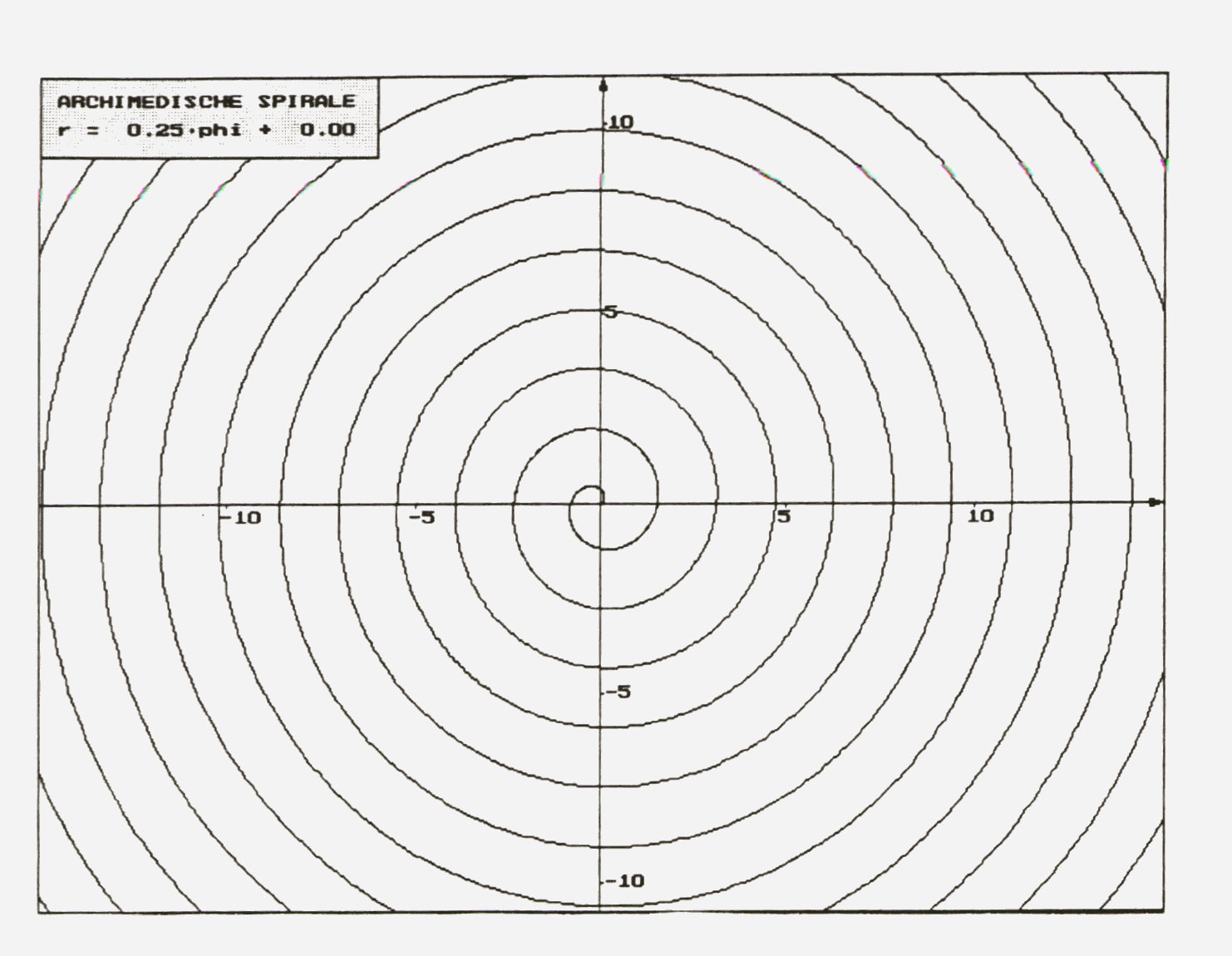Abb.3:
Archimedische Spirale
Man sieht, dass die Windungen der Archimedischen Spirale gleichabständig
sind. Mit anderen Worten: Aus allen Ursprungsgeraden schneidet diese Spirale
Strecken gleicher Länge aus. 
Beweis:
P
(
,r
), P
(
,r
) seien zwei Punkte auf dem selben
Strahl, jedoch auf zwei Nachbarwindungen der Archimedischen Spirale(
). Es gilt dann:
= 
= 
= 2a.
Zur Bestimmung der Tangente muss zunächst gesagt werden, dass man bei Kurven
in Polardarstellung zur Richtungsangabe der Tangente üblicherweise den
Winkel
zwischen dem
Fahrstrahl und der Tangente angibt, da dies die elegantere Darstellungsweise
ist. Es lässt sich zeigen, dass für den Winkel gilt:
tan
Für die Archimedische Spirale ergibt sich somit:
tan
Hierzu ist anzumerken,dass im Ursprung die Tangente und der Fahrstrahl
zusammenfallen. Da 
für 
,
streben Tangente und Fahrstrahl zwei zueinander senkrechten Geraden entgegen.
2.3. Flächenberechnung
Eine nicht uninteressantes Problem ist die Frage, welche Fläche die erste
Windung der Archimedischen Spirale einschließt. Auf dieses Problem wird im
Folgenden eingegangen. Auch hier muss wieder berücksichtigt werden, dass die
Spirale in Polarkoordinaten angegeben ist. Deshalb ist der übliche Vergleich
"x-mal so groß wie ein Quadrat mit der Fläche 1cm
" hier nicht besondes geeignet, man
bezieht sich besser auf einen Kreis(hier: Kreis mit dem am Ende der ersten
Windung der Spirale erreichten Radius).
Der Bezug auf eine andere Fläche stellt eine Erleichterung dar, da sich die Flächeninhalte so zueinander verhalten, wie die Volumina zweier Körper mit diesen Grundflächen und den gleichen Höhen. Abgesehen davon sind solche Körper wesentlich besser begreifbar, als der mathematisch Begriff der "unendlich dünne Fläche".
Um nun überhaupt diese "Cavalierische Umordnung" anwenden zu können, muss man sich zunächst eine geeignete Näherung für die Spirale überlegen. Hierzu betrachtet man nochmals das Raupenmodell, allerdings in leicht abgewandelter Form:
Es befinde sich nun nämlich ein Käfer auf dem Sekundenzeiger der Uhr. Der Unterschied zu dem ursprünglichen Modell besteht darin, dass sich der Sekundenzeiger nicht mit konstanter Geschwindigkeit bewegt, sondern jede Sekunde um ein Stück weiterspringt. Da sich der Käfer aber nur bewegen kann, wenn der Zeiger der Uhr stillsteht, ergibt sich nun keine Spirale mehr, sondern die folgende Bahn:
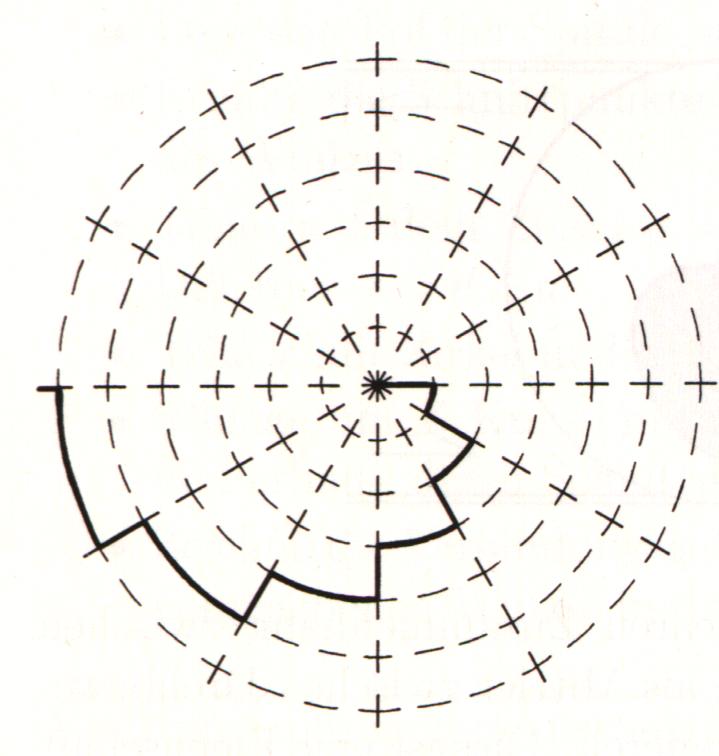
Abb.4 : Bahn des Käfers
Man unterteilt die Spirale nun gemäß dem Käfermodell in Sektoren, der Kreis wird in ebensoviele Sektoren unterteilt. Ordnet man nun die einzelnen Kreis-bzw.Spiralsegmente nicht nebeneinander, sondern übereinander an, so ergibt sich ein Zylindersektor bzw. ein stufenförmiger Turm mit verschieden großen Zylindersektoren, der sich durch immer größere Verfeinerung der Unterteilung der Spirale einem Kegelsektor nähert. Für jede beliebige Näherung haben die beiden Körper die gleiche Grundfläche und die gleiche Höhe. Durch Cavalierische Umordnung hat man so eine Möglichkeit gefunden, das Problem zu lösen, denn die Voluminaverhältnisse der oben beschriebenen Körper sind seit Archimedes bekannt. Man findet schließlich:
Die von der ersten Windung einer Archimedischen Spirale und dem größten Radius begrenzte Fläche verhält sich zu der des umschließenden Kreises wie das Volumen eines Kegelstücks zu dem eines Zylinderstücks gleicher Höhe und Grundfläche, also wie 1 zu 3.
2.4. Anwedungsbeispiel
" Wie lange ist ein Evergreen?"
Lieder stellen als eine zeitlich geordnete Abfolge verschiedener Geräusche
eindimensionale Objekte dar. Ziel der Technik ist es, diese Objekte auf
möglichst kleiner Fläche zu speichern. Eine gute Möglichkeit dazu stellte die
Schallplatte dar. Da eine konstante Winkelgeschwindigkeit leichter realisierbar
war, als eine konstante lineare Geschwindigkeit, wurden die Rillen auf der
Schallplatte in Spiralform angeordnet. Im Bereich eines Liedes ist der
Rillenabstand konstant, so dass es sich um eine Archimedische Spirale handelt.
Eine interessante Frage ist nun, welchen Weg der Tonkopf relativ zur
Schallplatte zurücklegt, oder, anders ausgedrückt, wie lange die spiralförmige
Rille ist. Als Beispiel hierzu betrachte man die Single "What a wonderful world"
von Louis Armstrong. Das Lied dauert t = 2,25min, die begrenzenden Radien sind
r
= 8,4cm und r
= 6,2 cm. Die konstante
Winkelgeschwindigkeit des Plattenspielers sei 
= 45/min. n sei die Anzahl der
Umdrehungen während des Liedes, also n = t = 45*2,25
101 Umdrehungen. Damit lässt sich
der Abstand b von aufeinenderfolgenden Windungen berechnen. Es ist
b = 
0,0218cm.
Im Vergleich zu den vorkommenden Radien ist b sehr klein. Man kann daher die
Archimedische Spirale in guter Näherung durch eine Schar konzentrischer Kreise
ersetzten, wobei der i-te Kreis der Schar den Radius r
hat. Für die Summe aller Bogenlängen
ergibt sich:
s
4625cm.
Das Lied ist also mehr als 46 Meter lang!!!
3. Die Logarithmische Spirale
3.1. Einleitung
In Kapitel 1 haben wir bereits die Definition einer Spirale behandelt, die wir uns noch einmal zu Gemüte führen wollen:
Definition:
Eine Spirale ist eine ebene Kurve, die aus unendlich vielen Windungen um einen festen
Punkt besteht und aus höchsten zwei Ästen zusammengesetzt ist, bei denen der
Abstand
vom Mittelpunkt streng monoton vom Drehwinkel abhängt.
Ein wesentlicher Aspekt hierbei ist die streng monotone Funktion (im folgenden mit
"f" bezeichnet) des Radius in Abhängigkeit vom Winkel.
In Kapitel 2 wurde als streng monotone Funktion einfach f(j )= a j benutzt mit jIR\IR, aIR und damit die
archimedische Spirale definiert.
Wir kennen aber noch eine Reihe anderer streng monotoner Funktionen und eine auch in anderen Bereichen der Mathematik sehr interessante Funktion ist die e-Funktion.
Wollen wir doch mal sehen, was wir erhalten, wenn wir die e-Funktion als streng monotone Funktion verwenden, also Kurven betrachten der Form:
r = c exp(aj ) mit jIR, a,cIR
Dazu betrachten wir folgende Grafik:
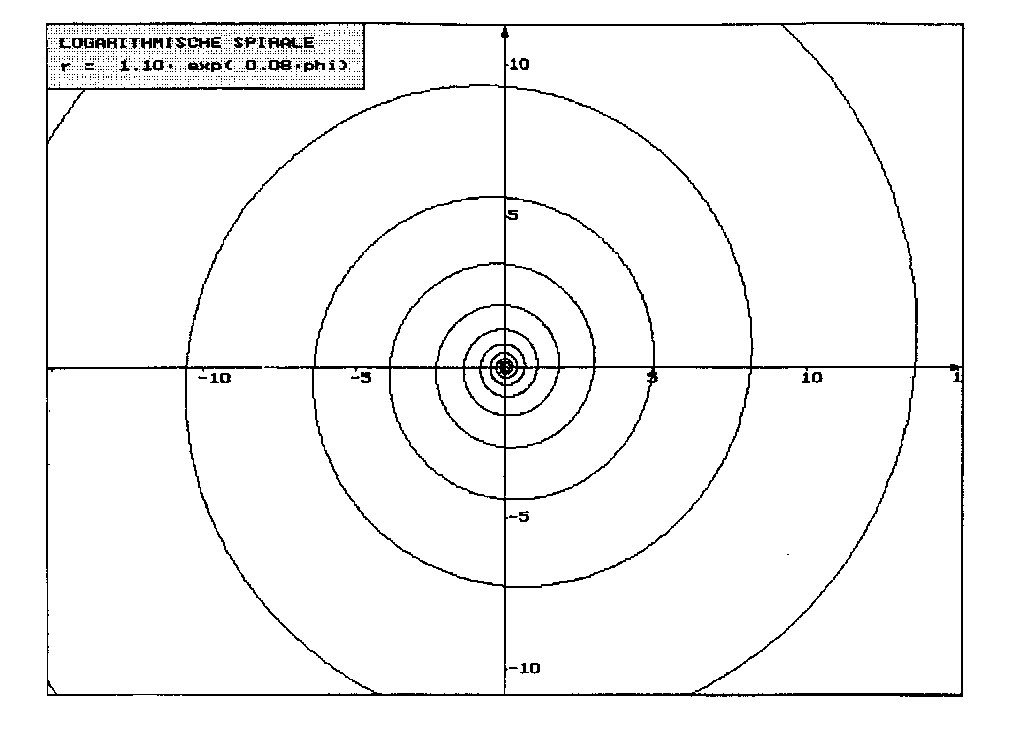
Abb: 3.1. Logarithmische Spirale
Die geplottete Kurve ist leicht mit unserer natürlichen Anschauung von Spiralen vereinbar.
Man nennt Spiraltypen von obiger Form "logarithmische Spiralen".
Diese treten vor allem bei Schnecken und anderen Schalentieren auf, was auf deren exponentielles Wachstum zurückzuführen ist.
Abb: 3.2 Schneckenhaus
Von Schneckenhäusern inspiriert, so vermutet man zumindest, hat der Grafiker und Maler Albrecht Dürer diese Spirale Anfang des 16. Jahrhunderts in sein Buch über Zeichenkunst aufgenommen. Darin sind zahlreiche Konstruktionsvorschriften für Spiralen enthalten, wobei die logarithmische Spirale dadurch identifiziert werden kann, dass er von einer Spirale sprach, deren Radien immer beim "Ineinanderlaufen" sich halbieren.
Verallgemeinern wir Dürers Konstruktion etwas und legen uns nicht auf Halbieren der Radien fest, sondern fordern die Radien sollen in einem konstanten Verhältnis stehen, wenn wir sie in konstanten Winkelabschnitten messen, so erhalten wir schnell eine charakteristische Eigenschaft der logarithmischen Spirale:
Satz:
Die bei konstanter Winkeldifferenz aufeinander folgenden Radien einer logarithmischen Spirale bilden eine geometrische Folge.
Beweis:
Sei (rn) eine Folge von Radien mit konstanter Winkeldifferenz a .
Zu zeigen: 
q.e.d.
Aufgeriffen wurde die logarithmische Spirale schließlich von René Descartes, Evangelista Torricelli und Jakob Bernoulli. Letzterer war von der logarithmischen Spirale so fasziniert, dass er von Ihr als dem "Sinnbild des Lebens und der Auferstehung" sprach. Bernoullis Faszination ging sogar so weit, dass er die Spirale eingemeiselt in seinen Grabstein wünschte.
Und wenn man sich jetzt vorstellt man wäre Steinmetz im 17.Jahrhundert und mit dieser Aufgabe konfrontiert gewesen, dann wäre uns wahrscheinlich der gleiche Fehler unterlaufen, der sich zugetragen hat. Bernoulli erhielt statt einer logarithmischen Spirale eine archimedische Spirale auf seinen Grabstein.
Damit uns so eine Greultat an einem genialen Mathematiker nicht passieren kann, lohnt es sich also noch einiges mehr über diese Spirale in Erfahrung zu bringen:
Wir wollen uns beispielsweise der Konstruktion einer logarithmischen Spirale zuwenden:
3.1. Konstruktion einer logarithmischen Spirale
Gegeben seien das Zentrum der Spirale und zwei Punkte auf der Spirale.
Wir konstruieren nun einen weiteren Punkt der Spirale durch Ausnutzen der geometrischen Zuwachs- bzw. Abnahmeeigenschaft unter Verwendung des geometrischen Mittels.
Es wird eine Konstruktionsbeschreibung gegeben, die mit dem Geometrieprogramm EUKLID vorgeführt wird, wobei auch eine Konstruktion im Unterricht mit Zirkel und Lineal realisierbar ist (vorausgesetzt beim Schüler werden hierbei Kenntnisse in der Konstruktion von Winkelhalbierenden, Mittelpunkten von Strecken und Lotfällen).
1) Zentrum und die beiden Punkte festlegen:
2) Winkelhalbierende von < AZB einzeichnen
3) Kreis um Z mit Radius [ZB]
4) Schnitt von diesem Kreis mit g ergibt Punkt C
5) Mittelpunkt M von [AC] bestimmen
6) Kreis um M mit Radius [MC] = [MA]
7) Lot in Z auf g mit Kreis aus 6) zum Schnitt bringen, Schnittpunkt ist D
8) Kreis um Z mit Radius [ZD]
9) Schnitt des Kreises aus 8) mit Winkelhalbierende aus 2) ergibt gesuchten
Punkt P
3.3. Weitere Eigenschaften der logarithmischen
Spirale
Sehr einfach einzusehen ist beispielsweise, dass die logarithmische Spirale im Gegensatz zur archmimedischen Spirale ihr Zentrum niemals erreicht.
Betrachten wir dazu nochmals die Formel der logarithmischen Spirale:
r = c exp(aj ) mit jIR, a,cIR
Man sieht, dass für 
gilt: 
, wobei r = 0 wegen dem asymptotischen Verhalten der e-Funktion niemals
erreicht wird.
Mit anderen Worten:
Satz:
Betrachtet wird eine logarithmische Spirale mit Zentrum im Koordinatenursprung.
In jedem noch so kleinen Ursprungskreis liegen unendlich viele Windungen.
Beweis:
Sei r0 der Radius eines beliebigen Ursprungskreises. Es muß gelten:
c exp(aj ) £ r0 Û exp(aj ) £ r0 / c Û aj £ ln (r0 / c)
Û
(*)
Die Ungleichung (*) hat unendlich viele Lösungen und für jede Lösung j0 ist auch j0
- n2p mit n 
eine Lösung, d.h. es liegen
ebenfalls unendlich viele Windungen innerhalb des Ursprungskreises.
q.e.d.
Eine weitere Erkenntnis über logarithmische Spiralen, die auch in der Natur zum Tragen kommt lautet:
Satz:
Die Winkel zwischen Radius und Tangente bei einer logarithmischen Spirale sind konstant.
Beweis:
Für den Winkel J zwischen Radius und Tangente gilt analog zu Kapitel 2:
tan
q.e.d.
Anwendung findet diese Erkenntnis zum Beispiel beim spiralförmigen Flug einer Motte um eine punktförmige Lichtquelle (Lampe), bzw. im geraden Flug bei einer annähernd parallelen Lichtquelle (Mond). Die Motte behält die Lichtquelle nämlich immer unter konstantem Blickwinkel im Auge:
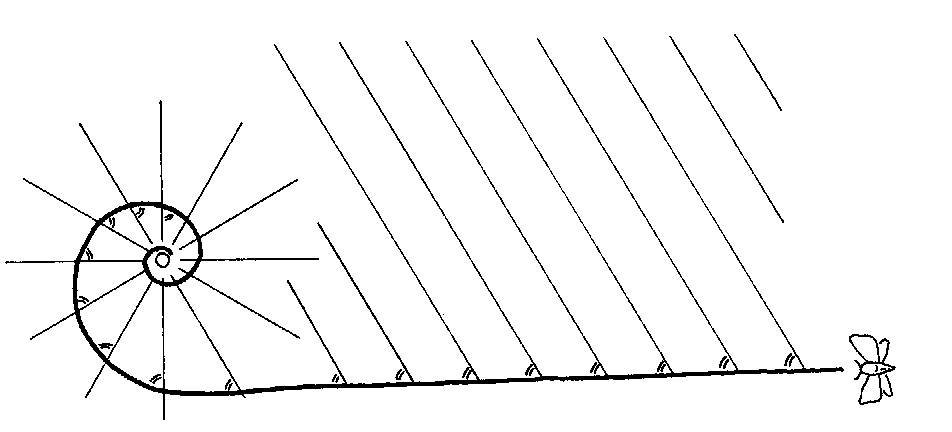
Abb: 3.3.Flug einer Motte
Wir wollen uns nun einem letzten Phänomen logarithmischer Spiralen nähern, nämlich der Tatsache, dass sie trotz unendlicher Windungszahl (im Innern) eine endliche Bogenlänge besitzen.
Betrachten wir dazu das Abrollen eines Kreises und einer logarithmischen Spirale auf einer Ebene:
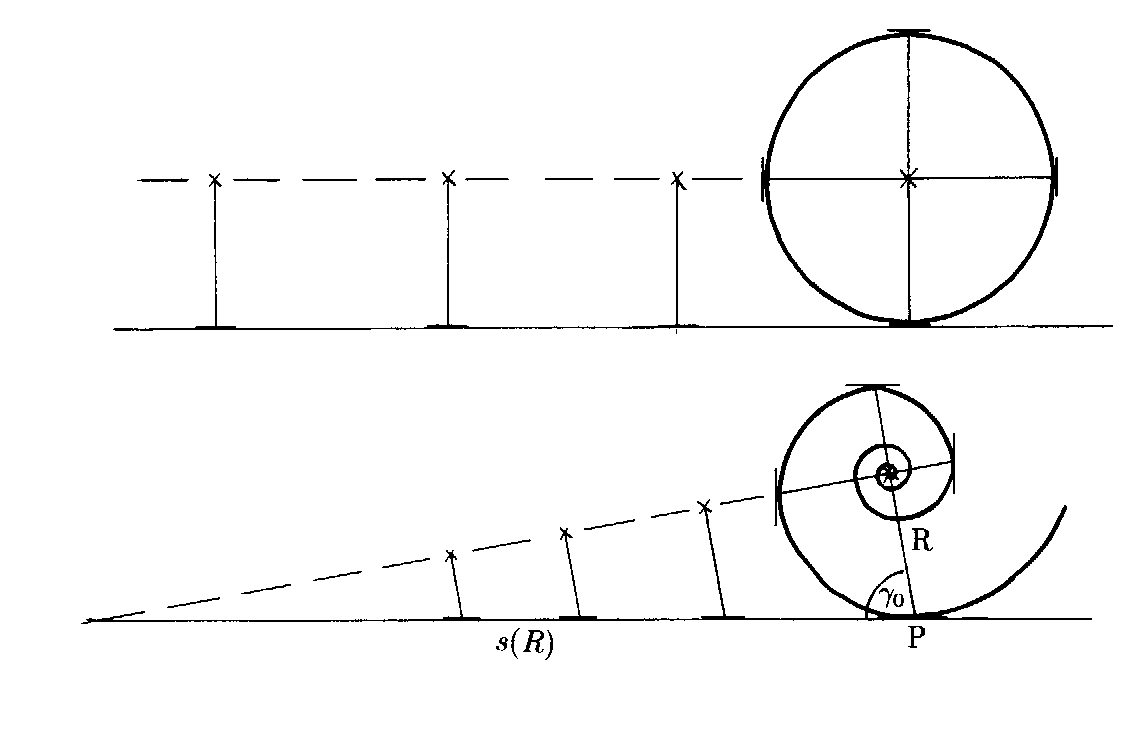
Abb: 3.4 Abrollen einer logarithmischen Spirale auf einer Ebene
Es ist leicht nachvollziehbar, dass der Mittelpunkt des Kreises parallel zur Ebene verläuft, während der Mittelpunkt der logarithmischen Spirale sich auf einer geneigten Abrollgerade befindet. Da diese Gerade nicht parallel ist, muß sie die Ebene irgendwann schneiden, das Zentrum der Spirale wäre also erreicht. Da aber der zurückgelegte Weg zwischen Anfangspunkt P und dem momentanen Auflagepunkt immer der Bogenlänge entspricht, würde das bedeuten, dass mit Erreichen des Zentrums auch die Bogenlänge endlich sein muß.
Satz:
Der Bogen einer logarithmischen Spirale im Bereich 0 < r £ R hat die Länge
Beweis:
Für die Bogenlänge gilt:
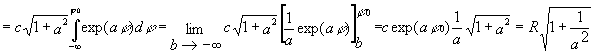
Wegen 
folgt 
q.e.d.
4. Überblick über Spiralentypen
Aus der Vielzahl der Spiralentypen werden nachfolgend noch einige Vertreter
kurz genannt und beschrieben. Hierbei sind die wichtigsten Elemente einer
mathematischen Untersuchung aufgelistet. Die für eine mathematischen Diskussion
der Kurven bedeutenden Größe sind mit Blick auf die jeweils günstigere
Beschreibung entweder in Abhängigkeit vom Polarwinkel oder in Abhängigkeit vom
Radius aufgeführt. Für Fläche und Bogenlänge sind die Differentiale angegeben,
aus denen sich konkrete Werte durch Integration in den jeweils gewünschten
Grenzen berechnen lassen. Aufgeführt sind noch stichwortartig die
Symmetrieeigenschaften und andere Besonderheiten der Kurven. Zur besseren
Orientierung werden - ohne Anspruch auf Vollständigkeit – zusätzlich Schlagworte
genannt, die auf das Auftreten der jeweiligen Spirale in Natur, Technik oder
Kunst (siehe auch Kapitel 1) hinweisen.
4.1 Hyperbolische Spirale
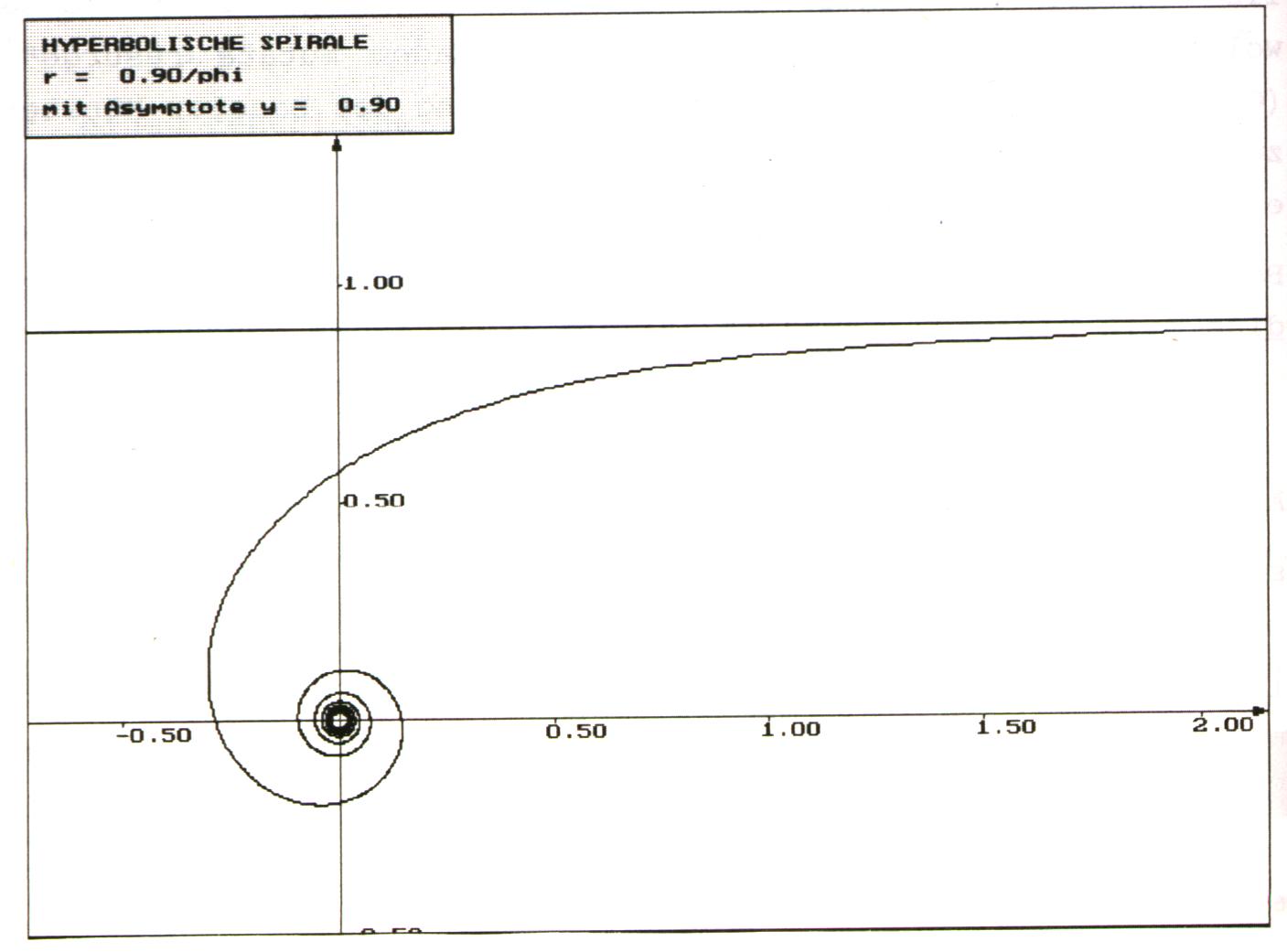
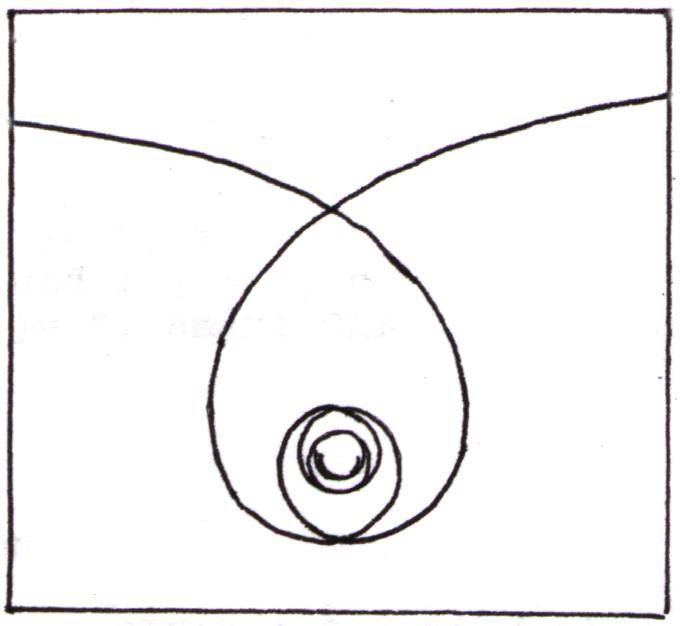
Diese Spirale hat die Polargleichung: r = a/j, a ¹ 0, j ,a Î IR+.
Es handelt sich hierbei um eine monoton fallende Polarfunktion. Weiter erkennt man an dem Adjektiv "hyperbolisch" eine Analogie zur Hyperbel, deren Gleichung y = a/x ist.
Die Hyperbolische Spirale hat das Zentrum 0 und die Asymptote y = a (was man auch gut an der obigen Grafik sieht).
Nachfolgend stichpunktartig noch einige wichtige Daten zu dieser Spirale.
dr
4.2 Fermatsche Spirale
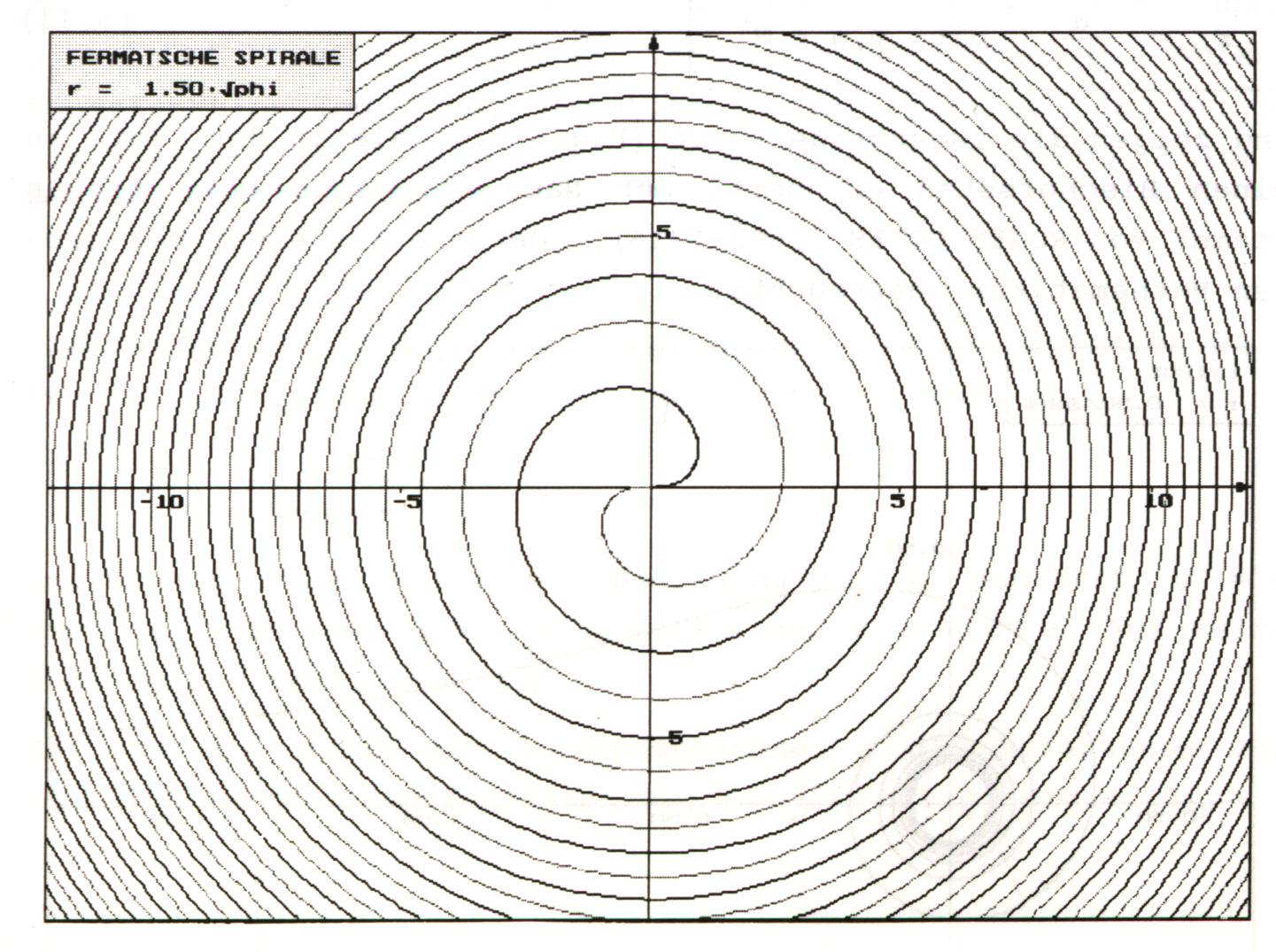
Ihren Namen erhielt diese Kurve von Pierre de Fermat (1601-1665). Im Jahre 1636 wird die Fermatsche Spirale durch die folgende Gleichung charakterisiert:
r2 = a2jbzw. r =
a* 
r = -a* 
mit a ¹ 0, j
Î IR \IR- , a Î IR
Es entsteht der Eindruck zweier ineinander verschlungener Kurven. Ihr
Ursprung liegt im Zentrum, was man auch leicht an der Grafik erkennen kann.
Weiterhin erkennt man, dass mit wachsendem j der
Windungsabstand abnimmt.
Einige Zusatzdaten zu der Fermatschen Spirale:
dr
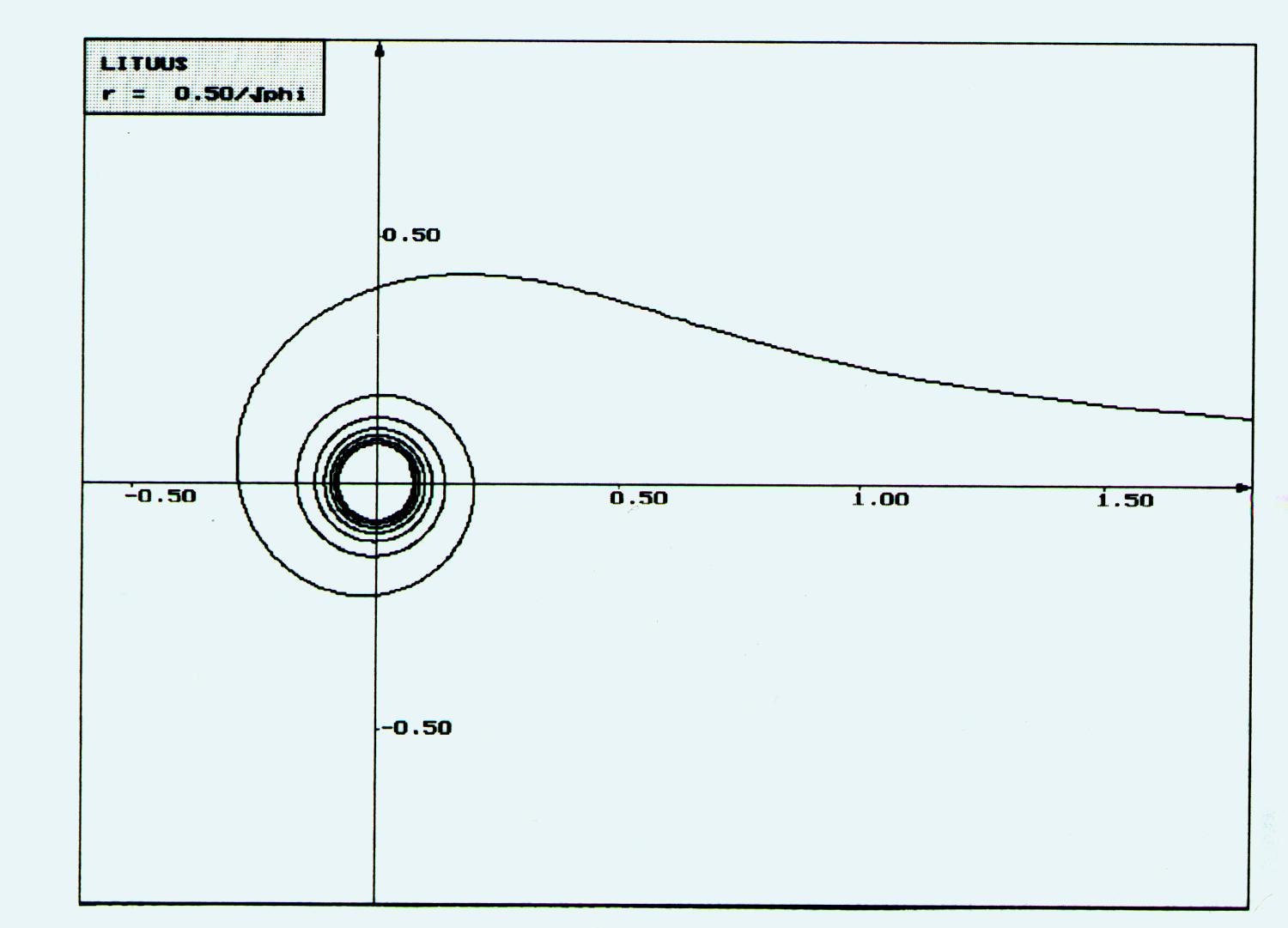
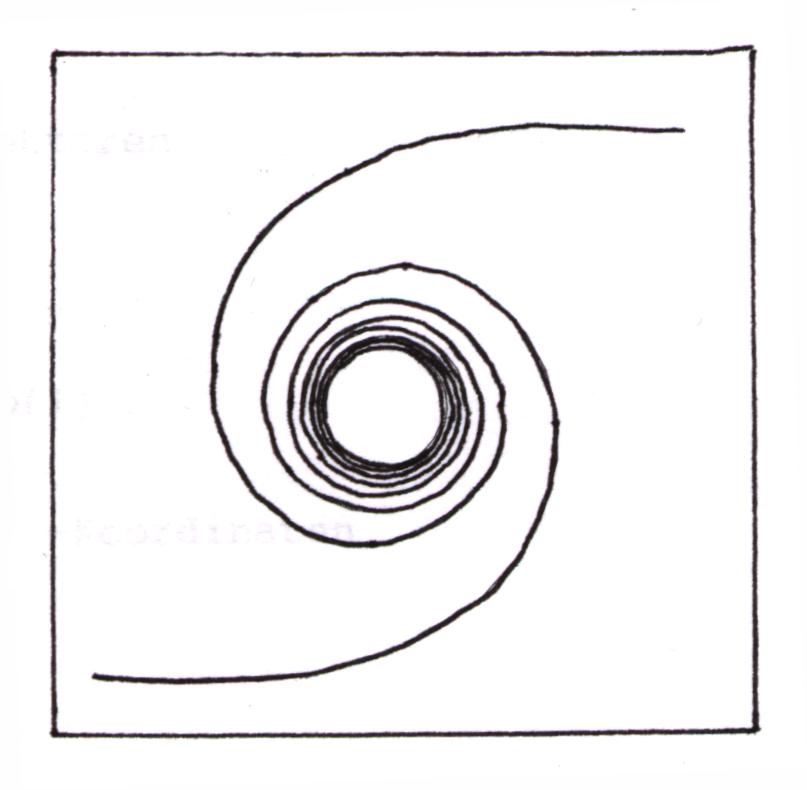
Beim Anblick dieser Kurve entdeckt man sofort die Ähnlichkeit mit einem Bischofsstab. Einer der ersten Mathematiker, der diese Kurve untersucht und benannt hat, war Roger Cotes (1682-1716). Der Krummstab hat folgende Gleichung:
r = a/
, mit
j , a Î IR+, a
¹ 0 bzw. mit seiner punktsymmetrischen Kurve:
r2 = a2/j, a ¹ 0.
Das Zentrum dieser Spirale liegt im Nullpunkt und die Asymptote ist y = 0.
Beweis:
Es gilt r® 0 für j® ¥ und r* sin j = a* sin j / 
® 0 für j ® 0. q.e.d.
Man kann weiter noch die Extremstellen und Extremwerte in bezug auf das
kartesische Koordinatensystem bestimmen, was hier aber zu weit führen würde. Der
Krummstab bzw. Lituus besitzt sogar einen Wendepunkt, was bei Spiralen eher
selten ist.
Abschließend noch einige interessante Daten zu diesem Spiraltyp:
dr
, ½)
Auf die drei folgenden Kurventypen wird nicht detailliert eingegangen. Sie gehören nicht zu den besonders interessanten Spiralen.
4.4.1 Galileische Spirale
dr
dr
dr
5.1 Thema Spirale im Schulunterricht
Nachfolgend wird untersucht, in welchem Maße das Thema Spirale tatsächlich im Schulunterricht vorkommt.
Wie bereits erwähnt sind Spiralen äußerst faszinierende Gebilde, die doch recht häufig auftauchen (z.B. Natur, Kunst, etc, vgl. dazu Kapitel 1). Trotz alledem ist es bedauerlich zu sehen, dass Spiralen in den derzeitigen Lehrplänen gar nicht, in denSchulbüchern nur selten und im tatsächlichen Unterricht kaum vorkommen.
Das liegt hauptsächlich daran, dass man in den Schulen die Einführung des
Polarkoordinatensystems vernachlässigt. Für die Darstellung der Spiralen sind
die Polarkoordinaten jedoch unerlässlich, denn als Bezugssystem dienen ein
fester Punkt, der Pol, und eine in diesem Punkt beginnende Halbgerade, die
Polarachse. Obwohl in der Schulmathematik viel von "Kurvendiskussion" die Rede
ist, steht dort seit langer Zeit der Funktionsbegriff im Vordergrund. Ein
weiterer Grund für das Nichtunterrichten des Themas Spirale ist, dass das
Zeichnen von Spiralen zu viel Zeit in Anspruch nimmt. Als Gegenargument hierzu
kann man anmerken, dass das Handkonstruieren der Archimedischen Spirale (mit
Hilfe eines Taschenrechners evtl. auch mit Polarkoordinatenpapier) den Schülern
doch zumutbar ist, schon allein als Einübung des Polarkoordinatensystems. In
unserer heutigen hochtechnisierten Zeit ist der Umgang mit Computern
unerlässlich, und muss bereits im Schulunterricht gefördert werden. Hierzu
bietet sich ein Computerprogramm zur Spiralenkonstruktion an, das den Kurven
selbst wieder zu mehr Bedeutung verhilft. Der zugrundeliegende Algorithmus ist
nicht allzu schwer verständlich, die programmtechnische Realisierung kann einer
der heute in nahezu jeder Klasse vorhandene "Computerfreak" übernehmen (siehe
dazu Java-Programm zur Spiralenerzeugung im Anhang). Somit wird noch nebenbei
das selbständige Erarbeiten von Sachverhalten entweder allein als Hausaufgabe
oder in der Schulstunde als Gruppenarbeit eingeübt. Wichtig bei dem
Spiralenthema ist der Vergleich der unterschiedlichen Spiralenarten, sowie das
Herausarbeiten ihrer Beziehungen untereinander und zu bekannten Kurven.
Wesentlich hierbei sind die Eigenschaften wie Windungsabstand, Verhalten an den
Definitionsrändern, etc. In diesem Zusammenhang ist es wichtig, dass es gar
nicht schwer fällt, neue Beispiele zu generieren. Man braucht nur dafür zu
sorgen, dass r = f (j ) stetig und monoton ist und sich
dabei an monotone Funktionen der Art y = f (x) zu erinnern.
5.2 Verschiedene Ansätze zur Einführung in die Spiralentheorie
5.2.1 Spiralen Zeichnen mit dem Zirkel (Archimedische
Spirale)
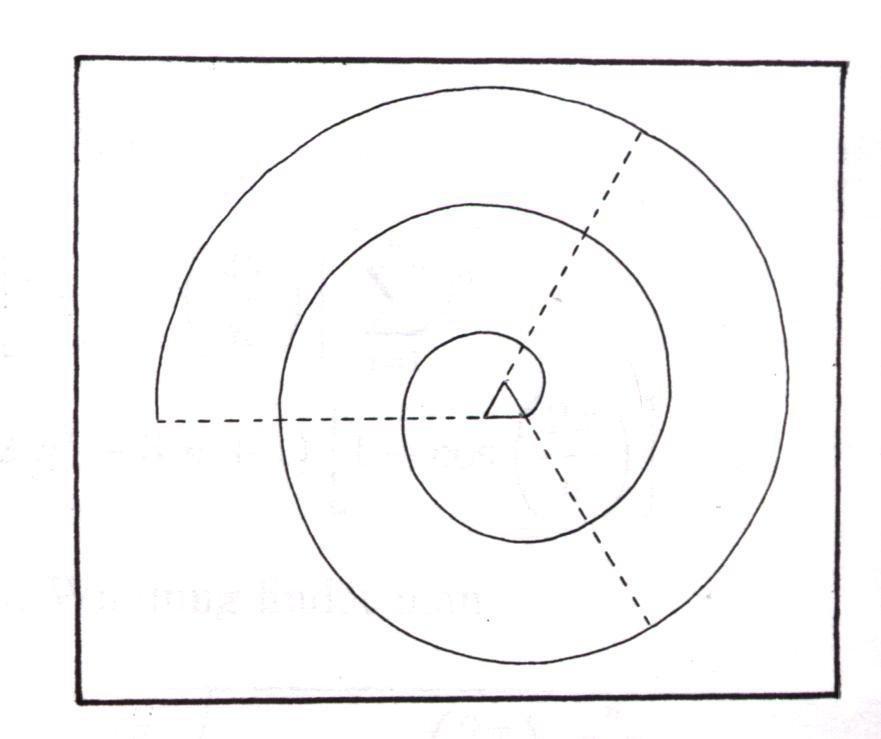
Folgendes Verfahren wird hierbei zugrunde gelegt:
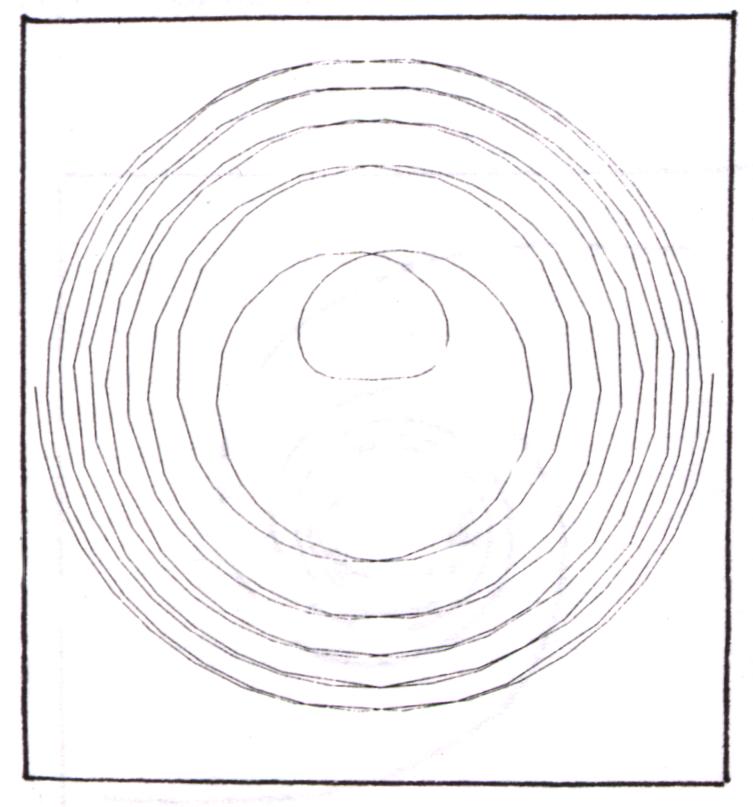
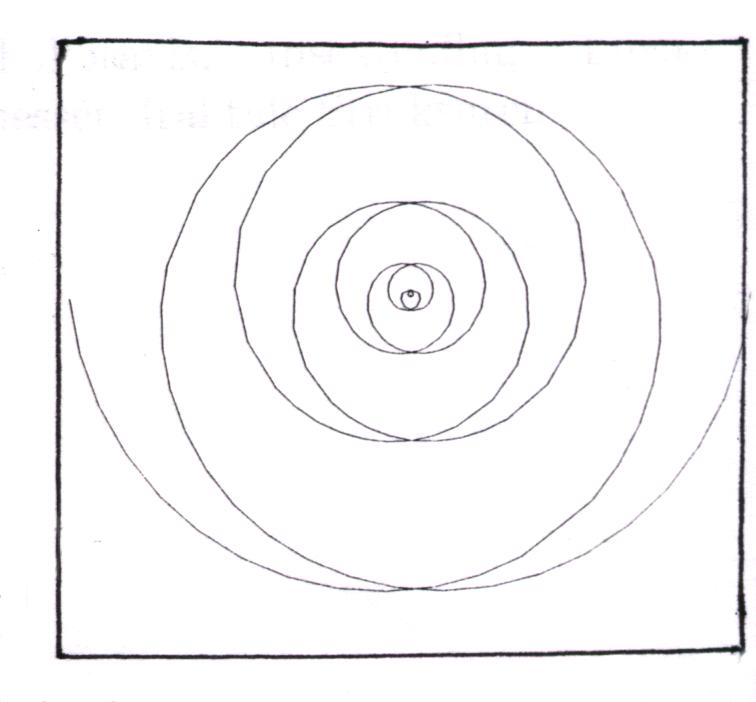
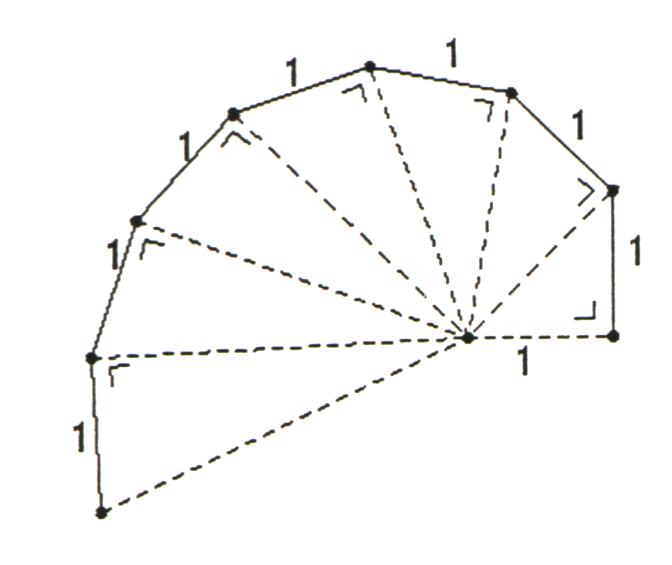
Als erstes konstruiere man ein gleichseitiges Dreieck und schlage um eines der Eckpunkte mit dem Zirkel einen Kreisbogen, der vom im Uhrzeigersinn benachbarten Eckpunkt ausgeht und auf der Verlängerung der nächsten Dreiecksseite endet. Zyklisch wechselnd setze man die Figur nun durch 120o- Bögen fort. Jeder dieser Kreisbögen beginnt im Endpunkt des vorangegangenen und endet im Schnittpunkt mit der Verlängerung der nächsten Dreiecksseite. Während der Radius bei jedem Schritt um eine Seitenlänge wächst, setzt man dieses Verfahren fort, bis die entstehende Spirale die gewünschte Größe hat.
Konstruktion:
1.)
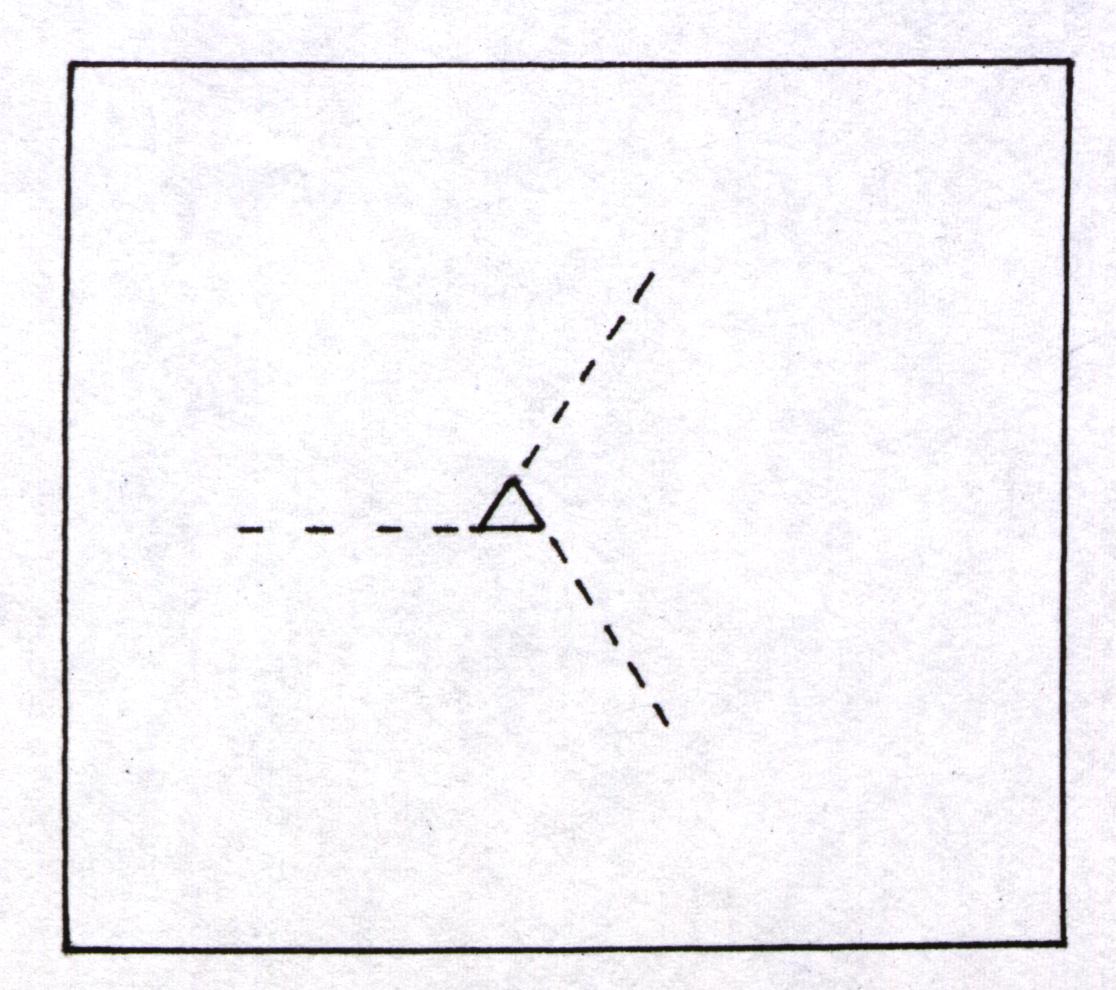
2.)
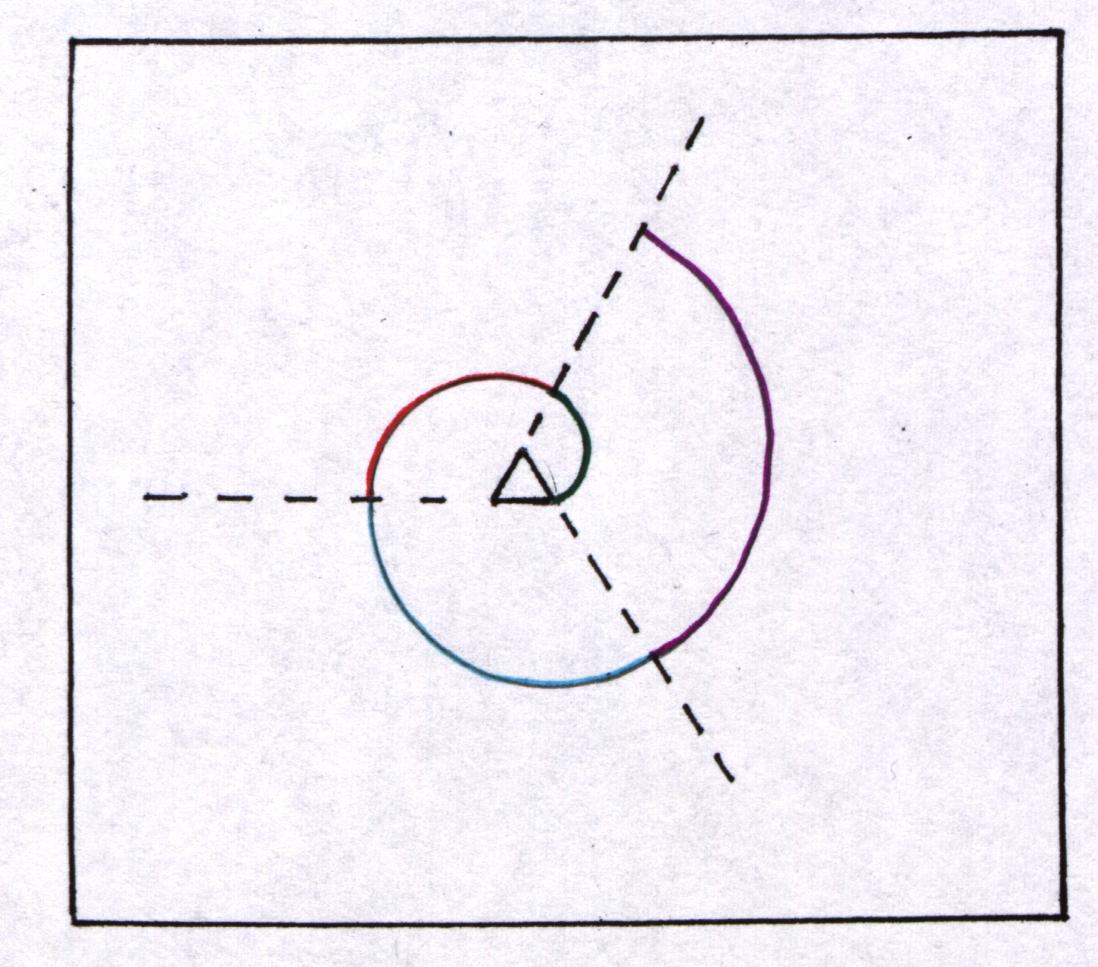
Farberklärung zu Grafik 2.):
(Archimedische Spirale)
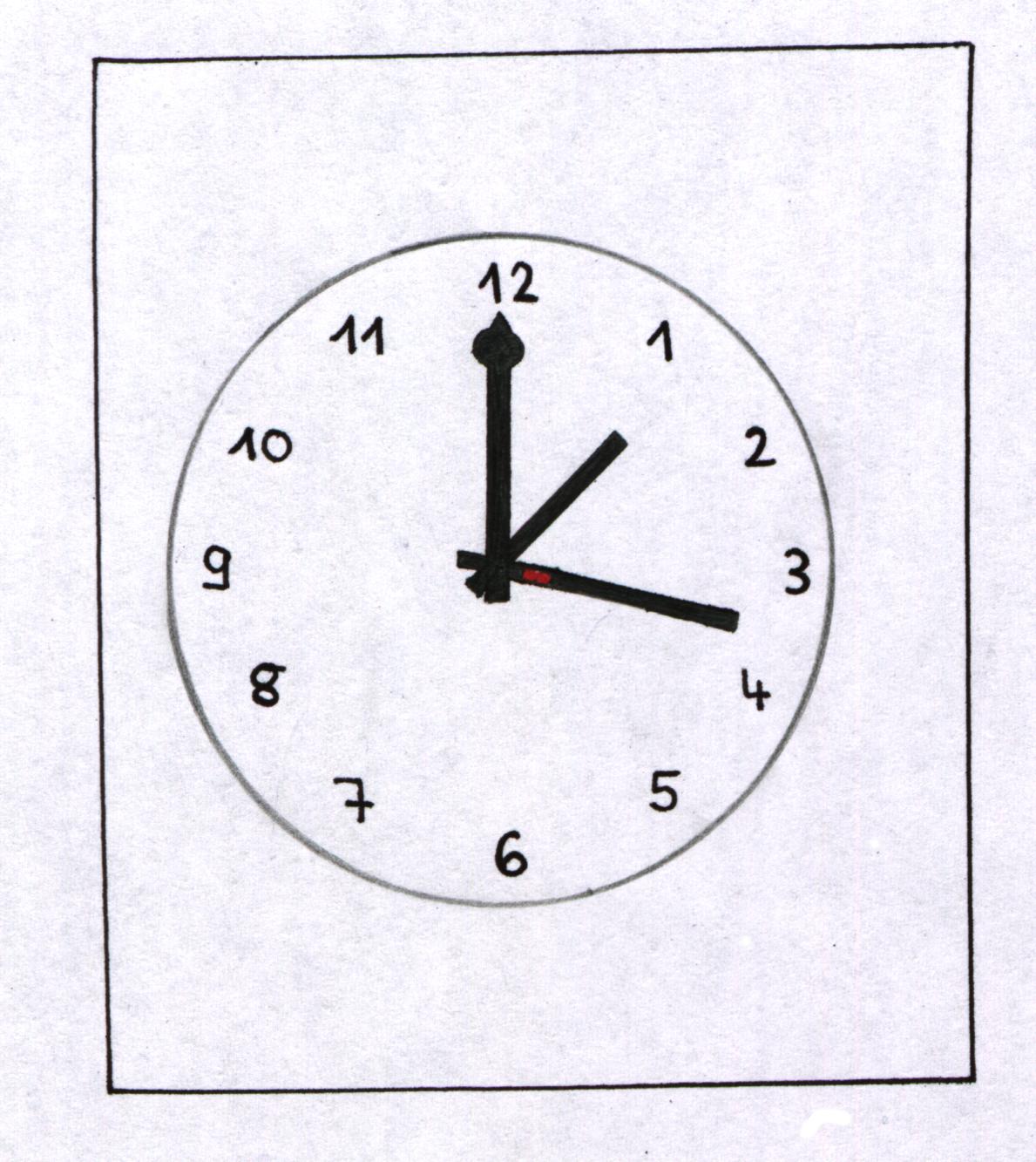
rot = Raupe
Anders als in Punkt 5.2.1 wird hier vorgegangen. Man versucht mit diesem Modell "Raupe auf der Uhr" den Schüler erst mal eher "unmathematisch" den Zugang in das Spiralenthema zu erleichtern. Dies sieht auf den ersten Blick sehr "trivial" aus, es steckt aber eine ganze Menge Mathematik dahinter.
Die Strategie dieses Modells sieht folgendermaßen aus:
Um 13.15 Uhr erwacht eine Raupe in der Mitte einer Kirchturmuhr auf dem Minutenzeiger und möchte dort nicht bleiben. Während der Minutenzeiger sich mit konstanter Winkelgeschwindigkeit um den Mittelpunkt dreht, kriecht die Raupe auf dem Zeiger mit konstanter Geschwindigkeit nach außen.
Frage: Welche Bahn beschreibt die Raupe relativ zur Uhrfläche? Oder, anders ausgedrückt: Welchen Weg muss ein Käfer nehmen, der sich auf dem Deckglas der Uhr befindet und aus Geselligkeit immer genau oberhalb der Raupe bleiben möchte?
Stände der Zeiger still, wäre die Bahn der Raupe eine Halbgerade vom Mittelpunkt nach außen. Bliebe die Raupe auf einem bestimmten Punkt des Zeigers sitzen, beschriebe sie einen Kreis von festem Radius um den Mittelpunkt der Uhr. Nun finden aber beide Bewegungen gleichzeitig statt. Da die Bewegungen stetig sind, wird auch die Überlagerung beider stetig und "vollkommen glatt" sein. Denkt man sich den Zeiger unendlich lang und beide Bewegungen endlos fortgesetzt, so wird die Raupe unendlich oft (nämlich in jeder Stunde einmal) um den Mittelpunkt der Uhr gedreht, wobei sie sich immer weiter von ihm entfernt. Während jeder vollen Umdrehung legt die Raupe auf dem Zeiger die gleiche Strecke zurück. Außerdem fällt mit zunehmender Entfernung der von der Raupe zurückgelegte Weg gegenüber dem durch die Drehbewegung des Zeigers verursachten immer weniger ins Gewicht: Weit außen bewegt sich die Raupe fast kreisförmig um den Mittelpunkt der Uhr. Ihre Bahn windet sich mit fortschreitender Zeit in immer weiteren, immer schwächer gekrümmten Bögen spiralförmig um das Zentrum. Die von der Raupe relativ zum Zifferblattbeschriebene (oder vom Käfer auf dem Deckglas zurückgelegte) Kurve stellt eine Archimedische Spirale ( siehe auch Kapitel 2) dar.
Spiralenkonstruktion:
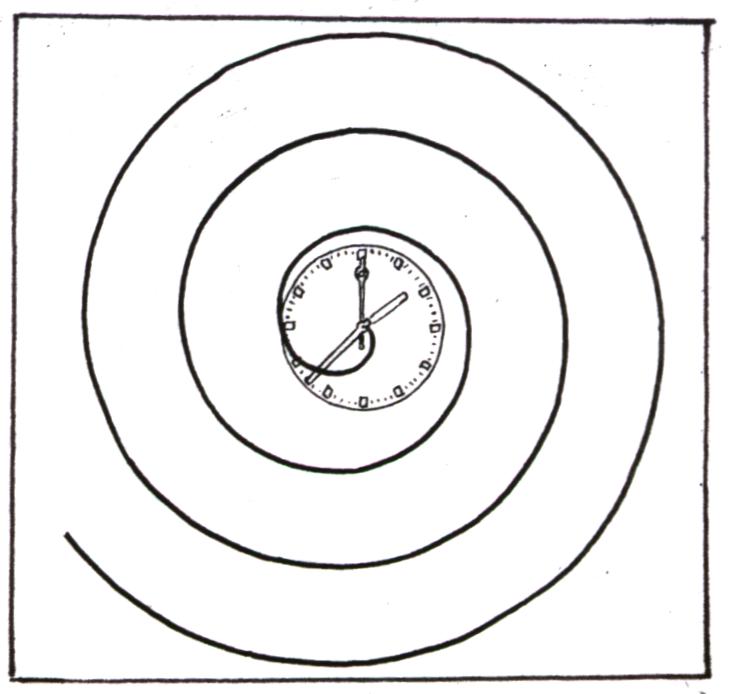
6. Konstruktion eines
"Spiralen-Zeichen-Gerätes"
Drehplatte
Bleistift-Transport-Wagen
Handkurbel (setzt Drehplatte und Bleistift-Transport-Wagen in
Bewegung)
Unser selbstkonstruiertes Gerät funktioniert, von der
Idee her, wie ein Schallplattenspieler. Es besteht aus einer Handkurbel die
gleichzeitig die Drehplatte und einen kleinen "Bleistift-Transport-Wagen", über
der Drehplatte, in Bewegung setzt. Es besteht eine feste Verbindung zwischen
Wagen und Drehplatte (Ketten, Wellen, Zahnräder). Der Wagen fährt mit konstanter
Geschwindigkeit von der Mitte der Drehplatte nach außen, zum Rand der Platte
oder in entgegengesetzter Richtung. Steigt die Plattengeschwindigkeit, steigt
auch die Geschwindigkeit des Wagens proportional und umgekehrt. Legt man nun
einen Bleistift in den Wagen, dann zeichnet dieses Gerät eine Archimedische
Spirale auf die Drehplatte.
Nicht unwesentlich, neben dem mathmatischen Bezug, bei
diesem Modell, ist der didaktische Hintergrund. Dieses Gerät wurde aus
Lego-Bauteilen konstruiert, die bestimmt für jeden Schüler noch ein Begriff
sind. Man versucht somit die Lernenden eher spielerisch zu motivieren, eigene
Modelle zu kreieren oder zumindest nachzubauen. Dies wäre vielleicht für eine
Hausaufgabe recht gut geeignet und es würde obendrein noch Spaß machen "mit Lego
zu spielen". Durch solch einen, eher (mathematisch) unüblichen Zugang, finden
Schüler vielleicht mehr Interesse und Motivation an dem Spiralen-Thema, wie
durch die "rein mathematischen" Einführungen.
7. Aufgaben
bekannt.
Java-Programm zur Spiralenerzeugung
/*
Datei............: Spirale.java
Kommentare.......:
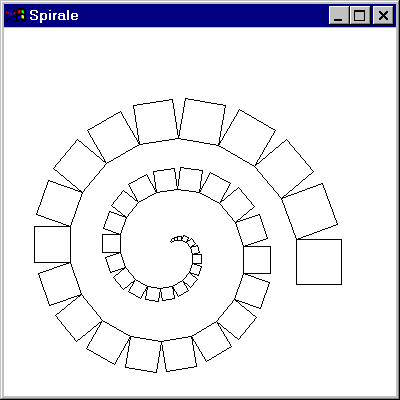
Die Darstellung der Spirale erfolgt, indem eine Folge von vielen
kleiner werdenden Quadraten ausgegeben wird, wobei nach jedem
Quadrat die Orientierung der Turtle um einen festen Winkel
verändert wird (in unserem Fall 20 Grad). Um das Ergebnis
etwas hübscher aussehen zu lassen, haben wir die Klasse
TurtleGraphics erweitert und mit der Fähigkeit versehen,
farbig gefüllte Polygone auszugeben. Nähere Beschreibungen
finden sich unten. Dies war zum Lösen der Aufgabe natürlich
nicht unbedingt nötig, eine einfache Liniengrafik hätte
auch genügt.
*/
import java.awt.*;
import java.awt.event.*;
public class Spirale
extends Frame
{
public static void main(String[] args)
{
Spirale wnd = new Spirale();
wnd.setSize(400,400);
wnd.setVisible(true);
}
public Spirale()
{
super("Spirale");
addWindowListener(
new WindowAdapter() {
public void windowClosing(WindowEvent event) {
System.exit(0);
}
}
);
setBackground(Color.lightGray);
}
public void paint(Graphics g)
{
int size = 30;
ColoredTurtleGraphics tg = new ColoredTurtleGraphics(g, this);
//100 Pixel nach rechts und 50 nach unten
tg.turnRight(90);
tg.moveForward(100);
tg.turnRight(90);
tg.moveForward(50);
tg.turnRight(180);
//Spirale zeichnen
tg.dropPen();
for (size = 45; size > 0; --size) {
//Quadrat zeichnen
tg.newPolygon();
for (int i = 0; i < 4; ++i) {
tg.moveForward(size);
tg.turnRight(90);
tg.addPoint();
}
//Durch ein farbiges Polyon überschreiben
tg.fillPolygon(new Color(0,255-5*size,20+5*size));
//An den Anfangspunkt des nächsten Quadrats
tg.moveForward(size);
tg.turnLeft(20);
}
}
}
/**
* Diese Klasse erweitert die Klasse TurtleGraphics um die
* Fähigkeit, farbige Polygone auszugeben. Dazu stellt es eine
* Art Transaktionsmechanismus zur Verfügung, mit dessen Hilfe
* eine Folge von Turtlebewegungen zusammengefaßt werden kann.
* Der Beginn der Folge wird durch Aufruf von newPolygon
* eingeleitet, nach jedem Schritt wird addPoint aufgerufen,
* und am Ende der Folge wird durch Aufruf von fillPolygon
* das umschließende Polygon mit der angegebenen Füllfarbe
* ausgegeben.
*/
class ColoredTurtleGraphics
extends TurtleGraphics
{
Polygon poly;
public ColoredTurtleGraphics(Graphics g, Container wnd)
{
super(g, wnd);
}
public void newPolygon()
{
poly = new Polygon();
}
public void addPoint()
{
poly.addPoint(state.actx, state.acty);
}
public void fillPolygon(Color color)
{
g.setColor(color);
g.fillPolygon(poly);
}
}
9.
Literaturverzeichnis
Archimedes : Werke- übersetzt und mit Anmerkungen versehen von Arthur Czwalina.
Wissenschaftliche Buchgesellschaft, Darmstadt, 1983
Baravalle, H. : Geometrie als Sprache der Formen. Verlag Freies Geistesleben GmbH,
Stuttgart, 1963
Blaschke, W. : Griechische und anschauliche Geometrie. Verlag von Oldenbourg,
München, 1953
Heitzer, J. : Spiralen ein Kapitel phänomenaler Mathematik. Ernst Klett Schulbuch-
Verlag, Leipzig, 1998
Hilbert, D./
Cohn-Vossen, S.: Anschauliche Geometrie. Springer, Berlin, 1932
Mainzer, K. : Geschichte der Geometrie. BI Wissenschaftsverlag, Mannheim, 1980
Meschkowski,H.: Mathematiker-Lexikon. BI Wissenschaftsverlag, Mannheim, 1980
Schupp, H./
Dabrock, H. : Höhere Kurven. Situative, mathematische, historische und
Didaktische Aspekte, BI Wissenschaftsverlag, Mannheim, 1995
Viète, F. : Einführung in die Neue Algebra, übersetzt und erläutert von Karin